First I need to put the definitions the author are using before asking the question itself. Polynomials have roots zeros where they are equal to 0.

Polynomials Intro Video Khan Academy
Yes it will always be a polynomial but depending on how many terms it has the answer may change.
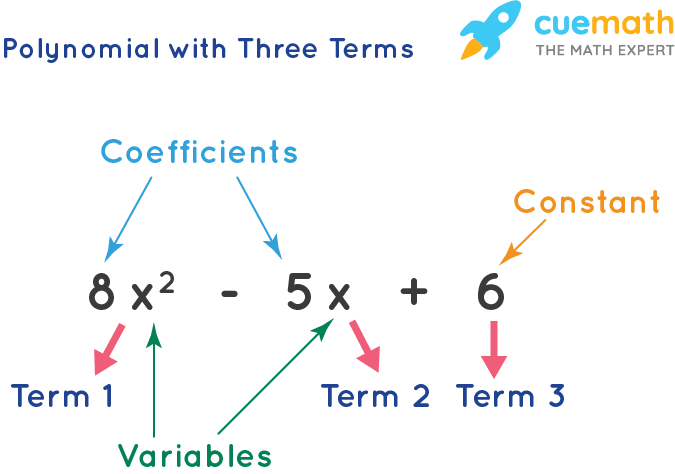
. A polynomial all of whose coefficients are zero is called an identical zero polynomial and is denoted by 0. That is p has at most zeros. A polynomial in a single variable x can always be written in the form.
How to use polynomial in a sentence. Example of a polynomial. To raise a base to a power keep the base and multiply the powers.
In the past Ive always jumped straight from definition of a polynomial to naming polynomials. This year I decided to add in two intermediate steps. So 2x 2x2 produces 1x which is not a polynomial.
X 2y3x 4y 5 x 2y3x 4y 5 3x 2 4xy 5x 6xy 8y 2 10y. Ax x5 1. Where a b and c are coefficients and d is the constant all of which are real integers.
Xy a x a y a. The highest order term has a positive coefficient otherwise it goes to zero at infinity eg. Find the zerosThe zeros of a function are the values of x that make the function equal to zeroThey are also known asx-intercepts.
Im following the book Number Systems and Foundations of Anaysis by Elliot Mendelson. Multiply each term in the first polynomial by each term in the second polynomial. The weighted degree of a monomial is the sum of all powers of the variables in the monomial each.
Zero polynomial linear polynomial quadratic polynomial and cubic polynomial. The Rule of Signs. Consider the number 6.
And always remember to add Like Terms. A polynomial is classified into four forms based on its degree. To find the zeros of a function you need to set the function equal to zero and use whatever method required factoring division of polynomials completing the square or quadratic formula to find the solutions for x.
Lets try an example. This value is equivalent to the exponent of the highest degree among all the terms that compose the polynomial. 2 is a polynomial of degree 0 so this example would appear to support the hypothesis in the question.
Remember that two polynomials ax and bx are equal iff corresponding coefficients are equal whereas two functions ax and bx are equal ax bx for every x in their domain. Its prime factors are 2 and 3. How do you multiply polynomial notes.
For our purposes it is convenient to use an alternative definition of the polynomial time computable functions. Key features of polynomial graphs. 2 times 3 6 so 6 divided by 2 is 3 and 6 divided by 3 is 2.
The polynomial time functions on ℕ are inductively defined by. The difference between 6x3 x2 - 4x 9 and 6x3 x2 - 4x 7 is 2. This one has 3 terms.
As we have already discussed in the introduction part the value of exponent should always be a positive integer. A special way of telling how many positive and negative roots a polynomial has. A polynomial equation is defined as an equation that has at least one algebraic term with at least one variable and all exponents are integers that are equal to or greater than zero.
Is a polynomial of degree n then the polynomial equation px 0 has at most distinct solutions. Px a 0 x n a 1 x n-1. Returns a new multivariate polynomial obtained from self by deleting all terms that involve the given variable to a power at least n.
And my kids have always struggled. For example consider the following two polynomials in mathbbZ_5x. Types of Polynomial.
X a x b x a b. Two polynomials are said to be equal if reduction of all similar terms makes them identical except for order and terms with zero coefficients. So no not always.
We can always check our factoring work by multiplying the factors to be sure we end up with the original polynomial. This is equivalent to saying that the graph of y p x x crosses the -axis at most times. To multiply monomials with the same base keep the base and add the powers.
A polynomial all of whose coefficients are zero is called an identical zero polynomial and is denoted by 0. I created this parts of a polynomial practice book for my students to work through at the beginning of our unit on polynomials. Weighted_degree weights.
Px a 0 x n a 1 x n-1. A polynomial in a single variable x can always be written in the form. Yes the difference of two polynomials is always a polynomial.
The meaning of POLYNOMIAL is a mathematical expression of one or more algebraic terms each of which consists of a constant multiplied by one or more variables raised to a nonnegative integral power such as a bx cx2. The most common definition of exponential time is. 2 polymonial n where polynomial is a polynomial that.
Polynomial division is closely related to multiplication and factoring. Return the weighted degree of self which is the maximum weighted degree of all monomials in self. A term is.
Thus a 5 th degree polynomial can have at most five x-intercepts. Two polynomials are said to be equal if reduction of all similar terms makes them identical except for order and terms with zero coefficients. Degree of the polynomial.
X a b x ab. Is not constant eg. To raise a product to a power raise each factor in the product to that power.
1 otherwise the time is also constant. Moreover any linear combination of two or more polynomials is a polynomial. These two notions of equality do not always coincide.
A polynomial equation is a sum of constants and variables. The graph of a polynomial function of degree n can have at most. In mathematics a polynomial is an expression consisting of indeterminates also called variables and coefficients that involves only the operations of addition subtraction multiplication and non-negative integer exponentiation of variables.
Roots are at x2 and x4. An example of a polynomial of a single indeterminate x is x 2 4x 7An example in three variables is x 3 2xyz 2 yz 1. And as we have already explained in the case of a polynomial function they will always be positive and integers.
A cubic equation is an equation involving. The equivalence of this definition is due to Cobham 1965. 1 term 1 term monomial times monomial To multiply one term by another term first multiply the constants.
2x 2 3x 1 0 where 2x 2 3x 1 is basically a polynomial expression which has been set equal to zero to form a polynomial equation. In the case of the polynomial fx 32 4x 2 the degree is equal to two. It has 2 roots and both are positive 2 and 4.
However polynomials cannot include negative exponents. 1 The following functions are polynomial time. Truncate var n.
A cubic polynomial has the generic form ax 3 bx 2 cx d a 0. A Polynomial looks like this.

Polynomials What Are Polynomials Definition And Examples

0 Comments